Content
Double Stars - A short introduction
Measurement of separation and position angle with small telescopes

Content
Double Stars - A short introduction
Measurement of separation and position angle with small telescopes

This article describes the Double Star Calculator (DSCALC) and its additional tools, including its usage, input data, and results.
The Double Star Calculator processes GAIA data records of two nearby stars, computes various results based on these records, and assesses the likelihood of the pair being a common proper motion (CPM) pair, a physical pair, or an optical pair. The Double Star Calculator – Orbital Elements generates orbit diagrams and a corresponding ephemeris table showing the separation and position angle of a double star, based on given orbital elements. The Double Star Calculator – Orbit Determination processes historical measurements of separation and position angle of a double star and attempts to determine its orbital elements. The Double Star Calculator – Convert Date & Time converts a given date and time into Julian Date and Besselian Epoch, and vice versa.
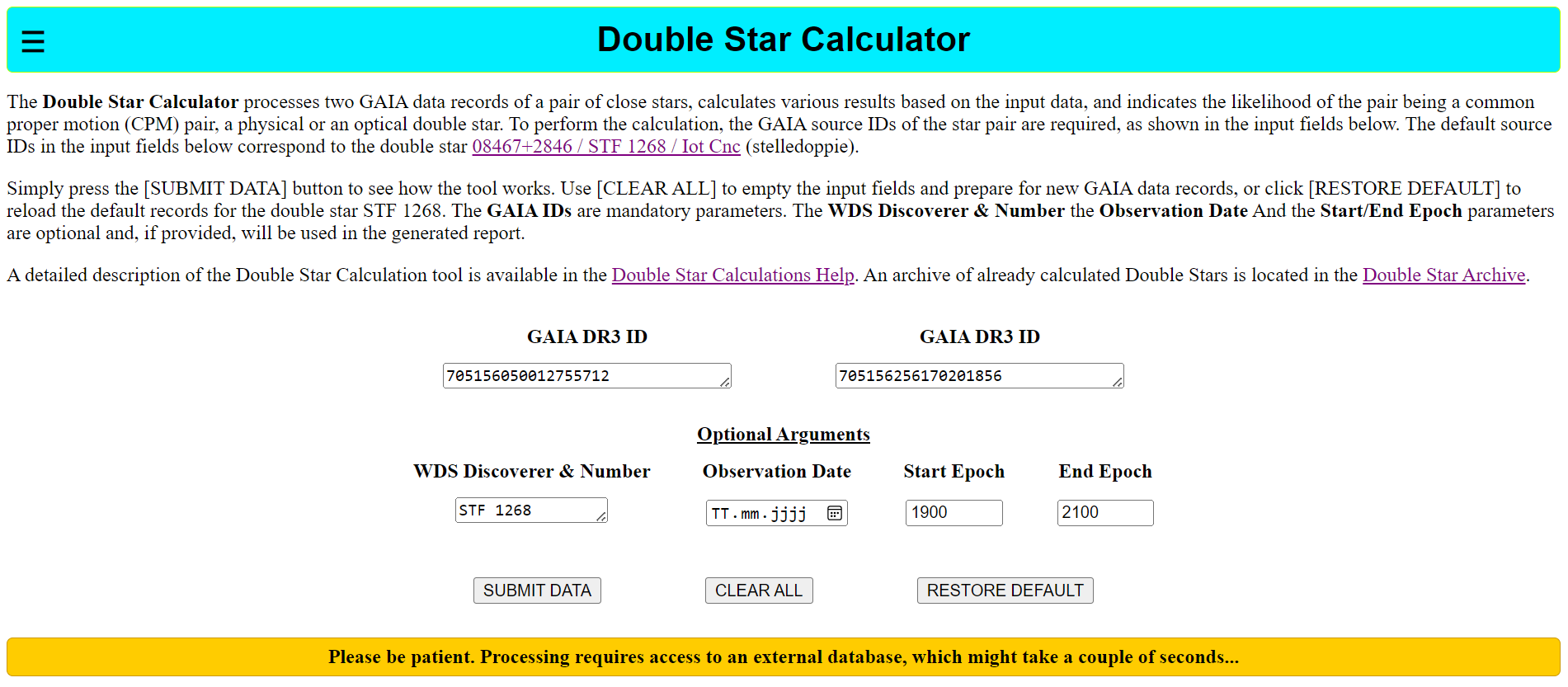
The Double Star Calculator just requires the Gaia DR3 Source-IDs of a pair of close stars as input parameters to calculate various results. Easy ways to obtain the Gaia DR3 Source-IDs are for example from the Aladin Sky Atlas (Desktop version) or from Cartes du Ciel / SkyChart.
Use [CLEAR ALL] to empty the input fields and prepare for new Gaia DR3 Source-ID values. Simply enter or copy and paste both Gaia DR3 Source-ID values into the two input fields of the Double Star Calculation tool. After entering the Gaia DR3 Source-IDs, click [SUBMIT DATA] to perform the double star calculations and display the results. Click [RESTORE DEFAULT] to reload the default Gaia DR3 Source-IDs for the double star STF 1268. The GAIA IDs are mandatory parameters. The WDS Discoverer & Number parameter is optional and, if provided, will be used in the generated report to access the USNO Washington Double Star Catalog (WDS) and display the corresponding entry. Additionally, the Observation Date parameter is optional and, if provided, will be used to calculate the separation and position angle of the pair for the corresponding epoch. If a dedicated Observation Date is not given, the current system date will be used instead. Finally, a Start- and an End-Epoch can be defined within the range J1500-J2500. These will be used to calculate the separation and position angle of the pair across this epoch range, based on the proper motion information in the Gaia records.
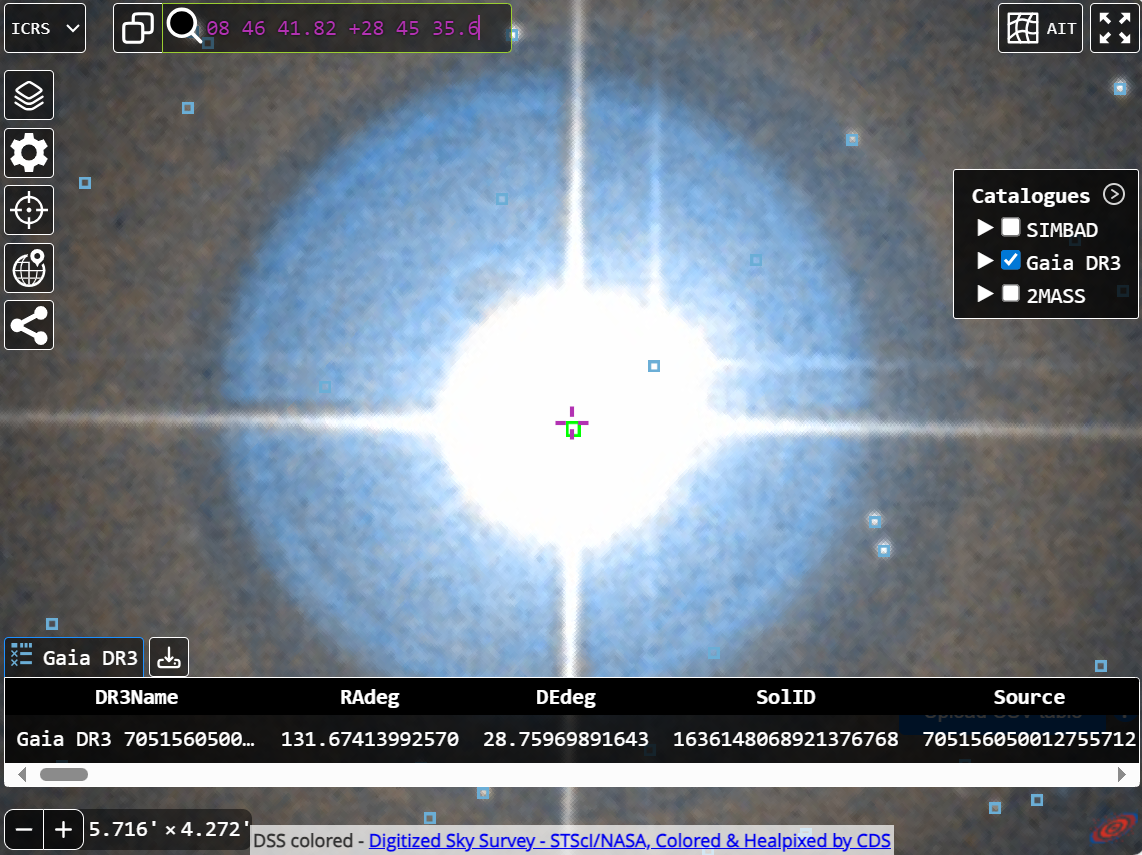
Unfortunately, there seems to be no database available online that provides a mapping between the WDS ID or Discoverer code and the corresponding Gaia DR3 source IDs of a double star. Therefore, this chapter shows an option to retrieve the Gaia DR3 source IDs based on the WDS ID or Discoverer code. The procedure itself is rather simple; the only tricky part is selecting the correct secondary. The procedure listed below is essentially the same when using the desktop version of Aladin.
Let's assume we are looking for the Gaia DR3 IDs of the double star STF 1268:
The Double Star Calculator computes results for a pair of stars based on the selected GAIA data records. Additionally, various parameters are calculated for each star individually. All calculations using GAIA data records are based on Epoch J2016, except for separation and position angle, where additional results are calculated for the specified epoch.
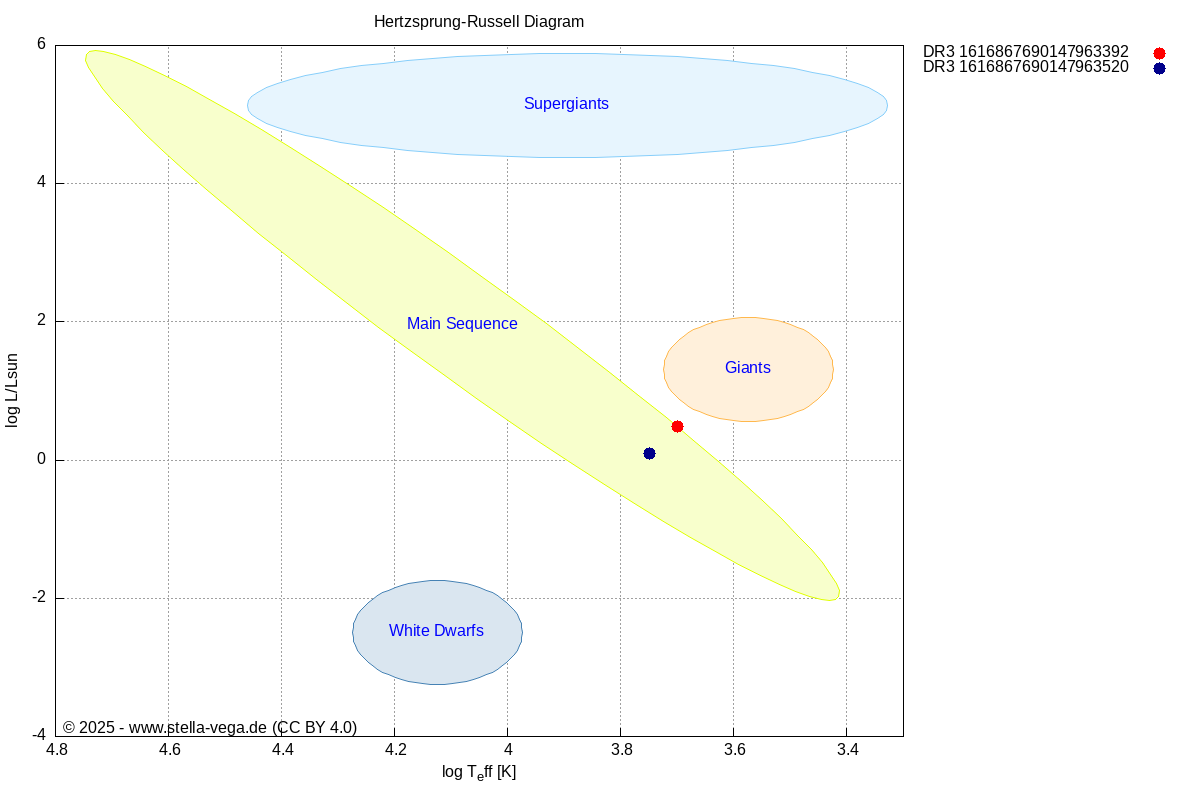
The positions of both components are plotted in a simplified Hertzsprung–Russell diagram (HRD).The positions are either derived from calculated luminosities and effective temperatures (Teff) from the Gaia GSP-Phot Aeneas library (plotted as solid circles) or estimated from the color index (bp_rp) measured by Gaia (plotted as open circles).
Finally a couple of plausibility checks are done with respect to get an indication if the checked pair is a physical, an optical or a CPM pair:
Check of Common Proper Motion
Check of Binarity
Check of RUWE parameters
Various Common Proper Motion indicators are calculated:
The likelihood of a stellar pair being a Common Proper Motion (CPM) system is represented via a twofold approach. The established method according to Harshaw (JDSO Vol. 12 No. 4, 2016) calculates a Ratio of Proper Motion (rPM), while a supplementary method determines a CPM Evidence Indicator. This indicator (ranging from 0.0 to 1.0) is derived by converting observed angular motion and radial velocity into a unified 2D/3D velocity vector in km/s. By incorporating parallax data, spatial separation, and projected separation, the calculation accounts for the physical scale and distance of the system, ensuring that the resulting evidence is physically meaningful.
Harshaw rPM Meaning CPM Evidence-Indicator Meaning
----------------------------------------------------- -----------------------------------------------------------------------------------
< 0.2 CPM (Common Proper Motion) 0.7 – 1.0 Strong High probability of physical association
0.2 - 0.6 SPM (Similar Proper Motion) 0.3 – 0.7 Moderate Potential association
> 0.6 DPM (Distinct Proper Motion) 0.1 – 0.3 Weak Low agreement, difference significant
< 0.1 Unlikely Significant discrepancy; association improbable
The Common Proper Motion (CPM) indication uses a fixed velocity cut-off of 5 km/s, implemented with a Gaussian-like function. CPM pairs are recognized within a radius of 1 parsec (the Jacobi radius).
Indicator | Value Meaning Unit
-----------------------------------|---------------------------------
rPM (Harshaw) : 0.04 (CPM) mas
CPM 3D Velocity Difference : 2.55 ± 0.13 km/s
CPM Velocity Evidence Indicator : 0.77 (Strong)
CPM Distance Evidence Indicator : 0.98 (Strong)
CPM Total Evidence Indicator : 0.87 (Strong)
rPM/CPM Agreement : High
In addition, the system evaluates the likelihood of binarity :
Fundamentally, the same Uncertainty-Weighted Likelihood approach is used to indicate a physical, gravitational relationship between the stars. In contrast to the CPM Evidence indication, different scaling factors are used to estimate the likelihood of binarity. The velocity cut-off is dynamic and based on gravitational scaling, with a benchmark of 2.1 km/s at 1000 AU. Potential binaries are recognized by the algorithm within a radius of 15,000 AU. If a potential binary is detected, the estimated orbital period at the lower bound, the escape velocity, and the circular orbital velocity are calculated. Additionally the Binding Energy Ratio is computed with ERatio <1 (bound) and >1 (unbound).
Indicator : Value
----------------------------------------------------------------------
Separation, Sigma and Reliability :
---------------------------------------
DS 3D Velocity Difference : 2.96 ± 0.06 km/s
Projected Separation : 64.11 AU
Spatial Separation : 5554.27 AU
1-Sigma Range : [ 3454.52, 7654.01] AU
Reliability : 2.64 SNR: LOW
Note: 3D distance not significantly resolved
Calculation with 3D spatial separation:
---------------------------------------
DS Velocity Evidence Indicator : 0.00 (Unlikely)
DS Distance Evidence Indicator : 0.87 (Strong)
Binarity Total Evidence Indicator : 0.00 (Unlikely)
Calculation with projected separation :
---------------------------------------
DS Velocity Evidence Indicator : 0.88 (Strong)
DS Distance Evidence Indicator : 0.99 (Strong)
Binarity Total Evidence Indicator : 0.93 (Strong)
Est. orbital period at lower bound : 419.00 years
Escape Velocity : 6.45 km/s (Bound)
Circular Orbital Velocity : 4.56 km/s
Binding Energy Ratio : 0.20 km/s (Strongly Bound)
Separation (AU) Orbital Period (1 + 1 M☉) (5 + 5 M☉) [years]
----------------------------------------------------------------
100 707 316
500 7906 3535
1000 22361 10000
2500 88388 39528
5000 249444 111803
10000 707107 316228
25000 2775042 1240347
50000 7905694 3162278
----------------------------------------------------------------
The Double Star Calculator estimates the probability of a star being part of a binary system based on the RUWE parameter, using the following mapping:
RUWE | Probability ------------------------------- Ruwe > 5 | Very high Ruwe < 5 | High Ruwe < 3 | Medium Ruwe < 1.4 | Low Ruwe < 1.25 | Zero
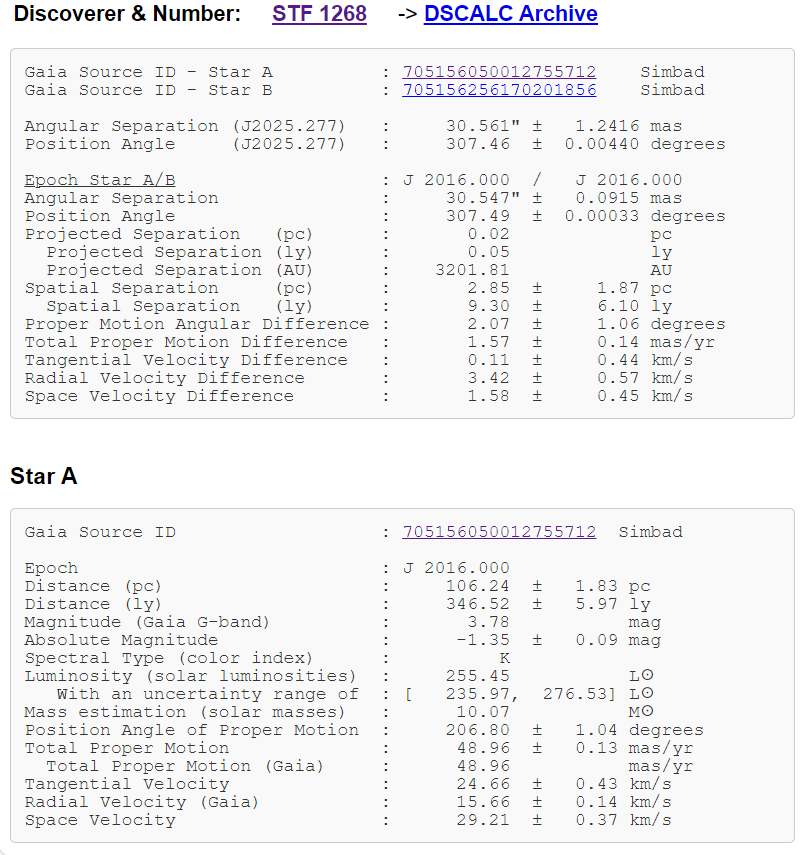
Finally, the Gaia data records used to calculate the results are displayed. By default, these records are collapsed. To view them, simply expand the section. Additionally, if the discoverer code and number were provided, the corresponding entry from the USNO WDS catalog is shown.
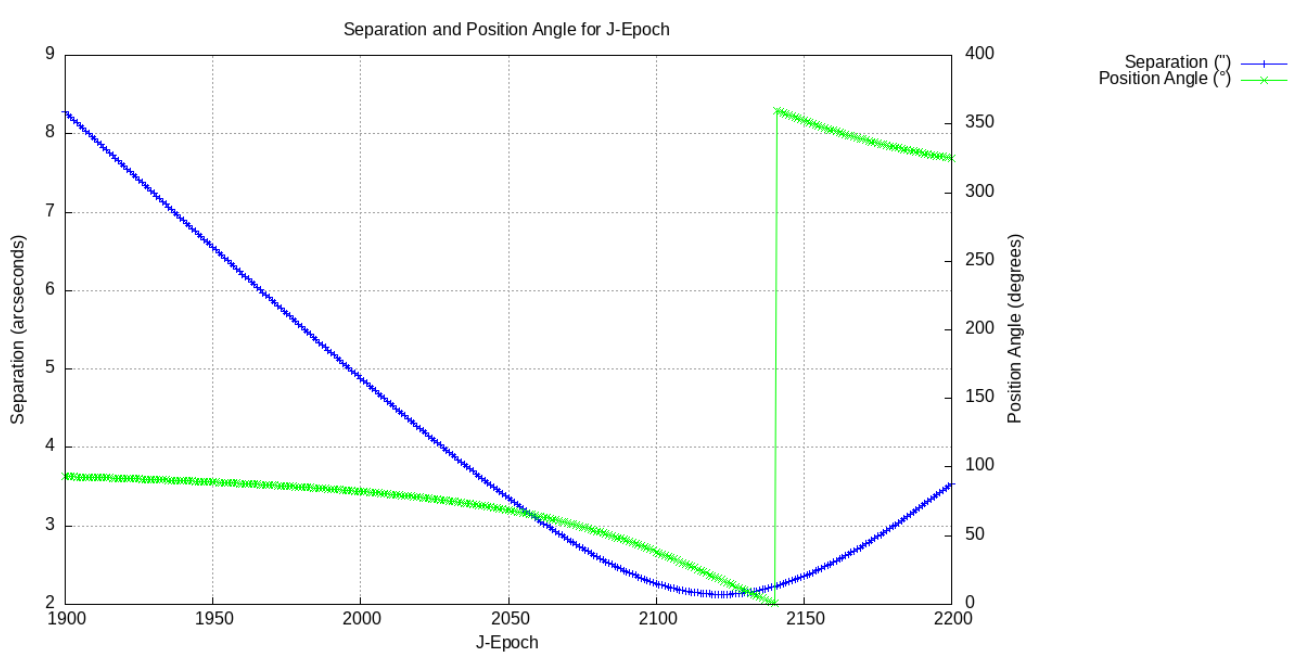
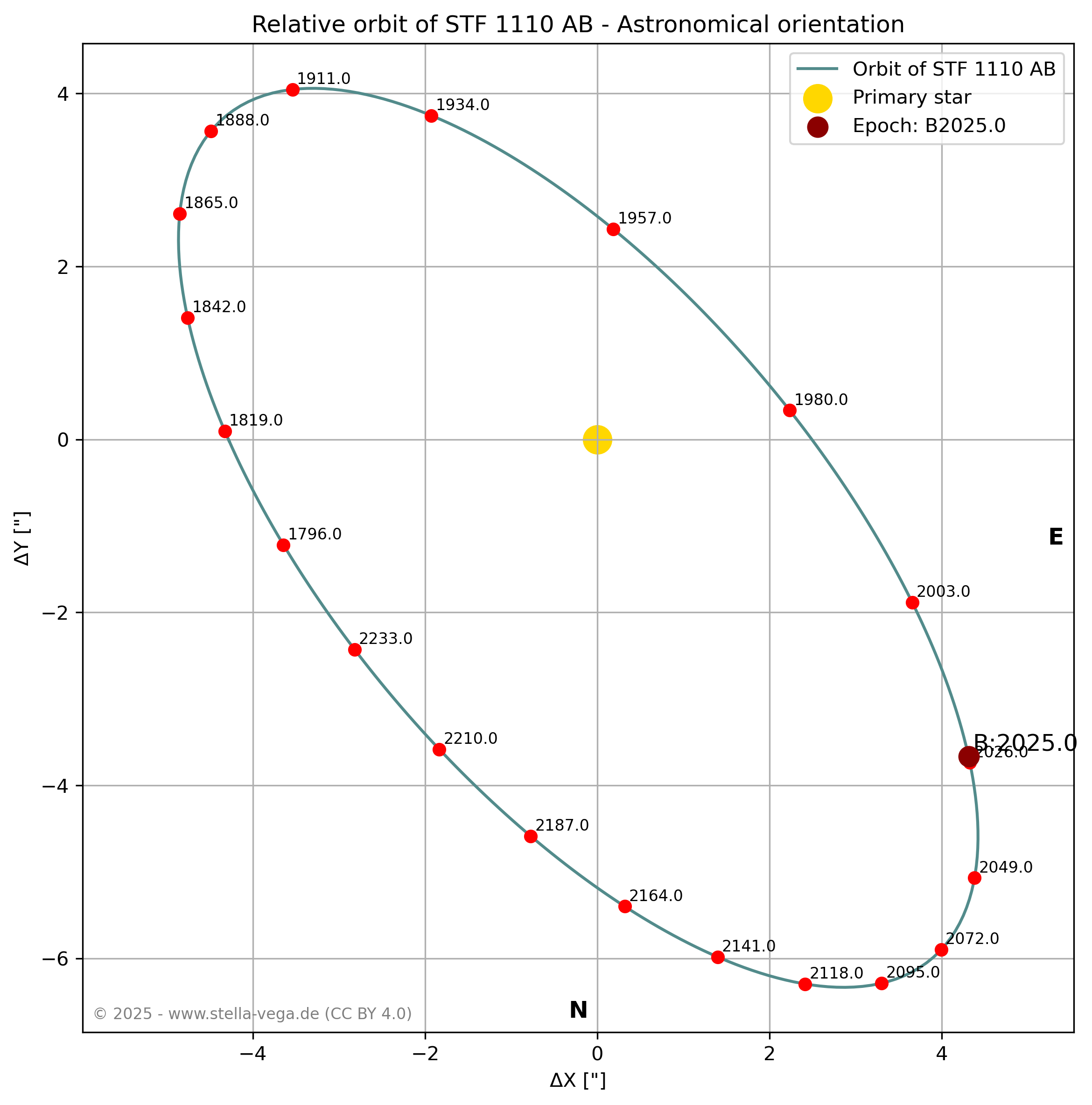
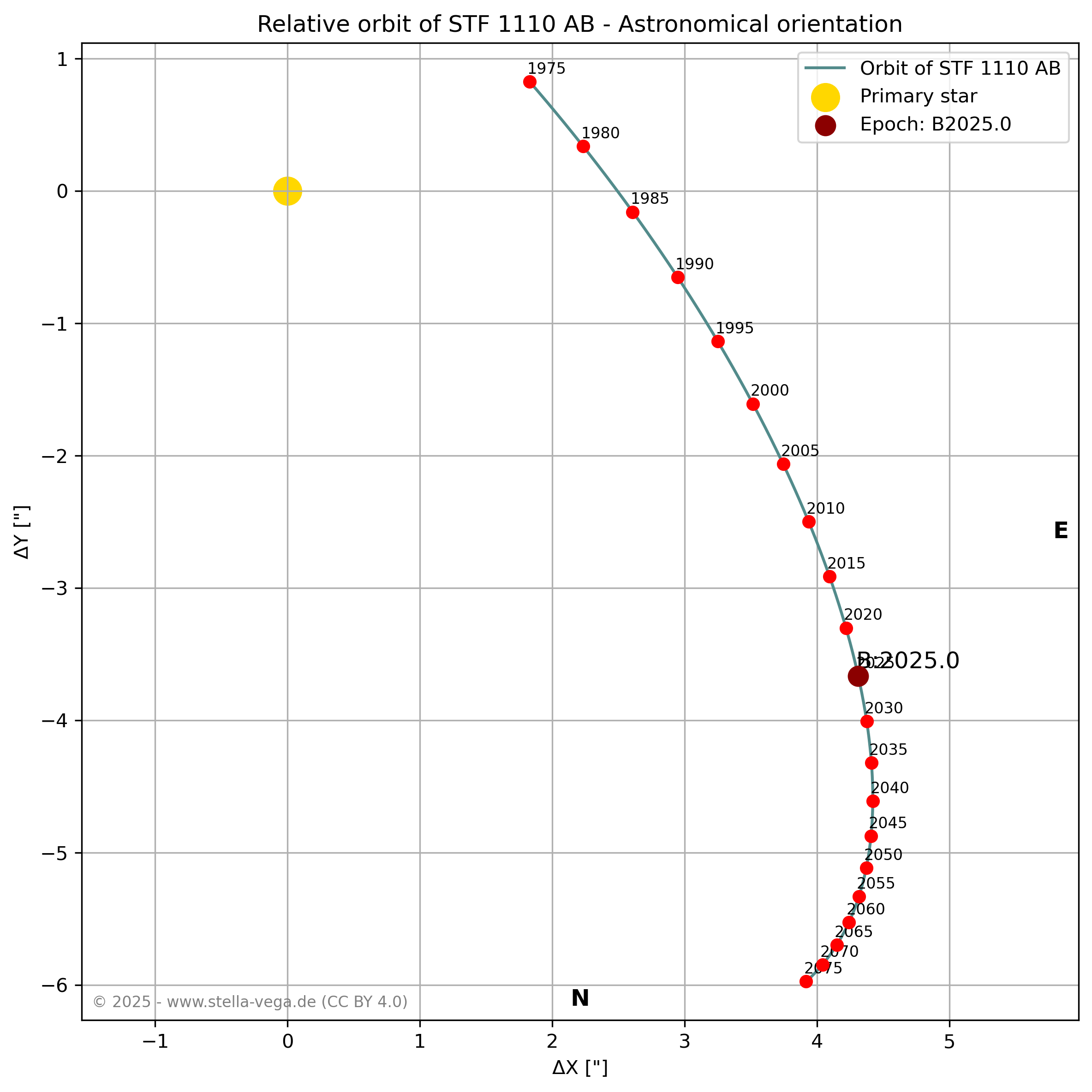
The Double Star Calculator – Orbital Elements generates an orbit diagram and a corresponding ephemeris table showing separation and position angle of a double star based on orbital elements.
There are two ways to calculate the ephemeris and generate the orbit diagram. The easiest method (Option 1) is to enter the discoverer code of a double star listed in the WDS Sixth Catalog of Orbits of Visual Binary Stars and click the [SUBMIT DATA] button. The tool will search the catalog for the discoverer code and, if a matching entry is found, extract the necessary data and calculate the orbit. The orbit and ephemeris are automatically calculated for a full orbit.
The field Current Epoch is used to calculate an ephemeris entry for the specified epoch. If the Current Epoch field is left empty, the system date will be used instead.
Simply press [SUBMIT DATA] to see how the tool works using the default data for the double star STF 1110 AB (Castor). Use [CLEAR ALL] to empty the input fields and prepare for new orbital elements, or click [RESTORE DEFAULT] to reload the default data.
The alternative method (Option 2) is to manually enter all required data into the form below. This offers greater flexibility regarding the input. If the fields Start year and End year are not set, the orbit and ephemeris are automatically calculated for a full orbit. By setting Start year and End year, parts of the orbit can also be calculated with higher precision. Press the [SUBMIT DATA] button to start the calculation.


If Option 1 is selected and orbital elements are also entered in the fields of Option 2, the manually entered elements will overwrite those retrieved from the Sixth Catalog. This feature provides greater flexibility and is useful to adapt certain orbital elements if measurements do not fit the calculated orbit.

The Double Star Calculator – Orbit Determination processes historical measurements of the separation and position angle of a double star and attempts to determine its orbital elements. To perform the calculation, a whitespace-separated list of measurements is required. Each line must consist of three entries: the Besselian epoch of observation, the measured separation in arcseconds, and the measured position angle in degrees.
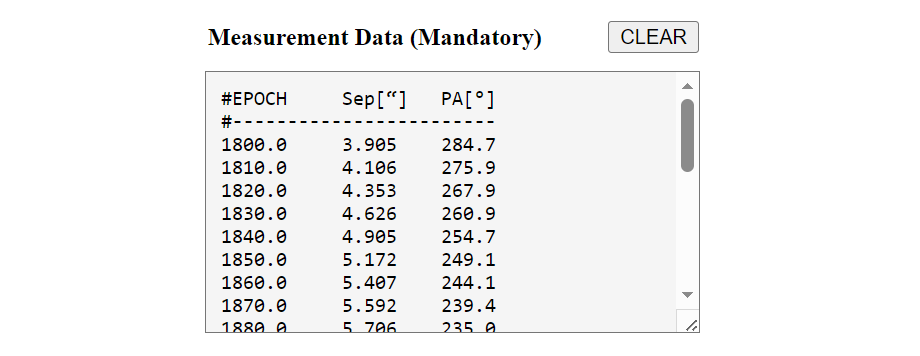
The parameter section Initialization with Orbital Elements is enabled if the Initialization parameter is set to Orbital Elements. In this case, the entered orbital elements are used as an initial guess for orbit determination. This is, for example, useful for refining an existing orbital solution.
Important note:
The number of measurements and the number of selected seeds have a significant impact on the processing time, which may take up to several minutes.

The Verbose verbose level adds the bounds for the orbital elements and the initial guess used for the calculation. The highest verbose level, Very Verbose, adds further details to the report in an expandable box, specifically internal details and intermediate results of the orbit calculation.


The Optimization Summary provides quantitative measures describing the quality, robustness, and statistical consistency of the orbit determination based on the supplied observations and measurement uncertainties. It should be interpreted as a whole. Individual metrics are most meaningful when considered together, particularly in relation to the number of observations, the orbital phase coverage, and the assumed measurement uncertainties.
Number of observations used in the orbit determination. Each observation consists of a measured separation (ρ) and position angle (θ), contributing two residuals (x and y) to the fit.
Time interval covered by the observations, defined by the minimum and maximum observation epochs. A larger time span generally improves orbit determination, especially for long-period systems, as it increases orbital phase coverage.
The total chi-squared value of the fit, defined as the sum of squared, uncertainty-weighted residuals. χ² measures the overall disagreement between the model and the observations.
Number of independent residuals available to evaluate the fit after accounting for the fitted model parameters. A positive and sufficiently large number of degrees of freedom is required for a meaningful statistical interpretation of χ² and reduced χ².
The reduced χ² indicates how well the orbital model matches the observations relative to the assumed measurement uncertainties.
Root-mean-square (RMS) residual of the separation (ρ), calculated from the differences between observed and modeled separations. This value quantifies the typical deviation of the observations from the model.
Root-mean-square (RMS) residual of the position angle (θ), calculated from the differences between observed and modeled angles. The RMS position angle is given in degrees and reflects the typical angular discrepancy between the model and the observations.
Maximum absolute residual of the separation (ρ). This value highlights the largest individual deviation between an observed separation and the corresponding model prediction.
Maximum absolute residual of the position angle (θ). This value highlights the largest individual deviation between an observed position angle and the corresponding model prediction.
Fraction of the orbital period covered by the observations, where P is the fitted orbital period. Values close to or exceeding one full period generally provide stronger constraints on the orbital elements, while smaller values indicate limited phase coverage and potential parameter degeneracies.
Double stars are characterised by the separation ρ (RHO), the distance between the components measured in arc seconds ["] and the position angle θ (THETA), measured in degrees [°] from 0°..360°, starting in the north via east, south and west. The origin is the brighter component.
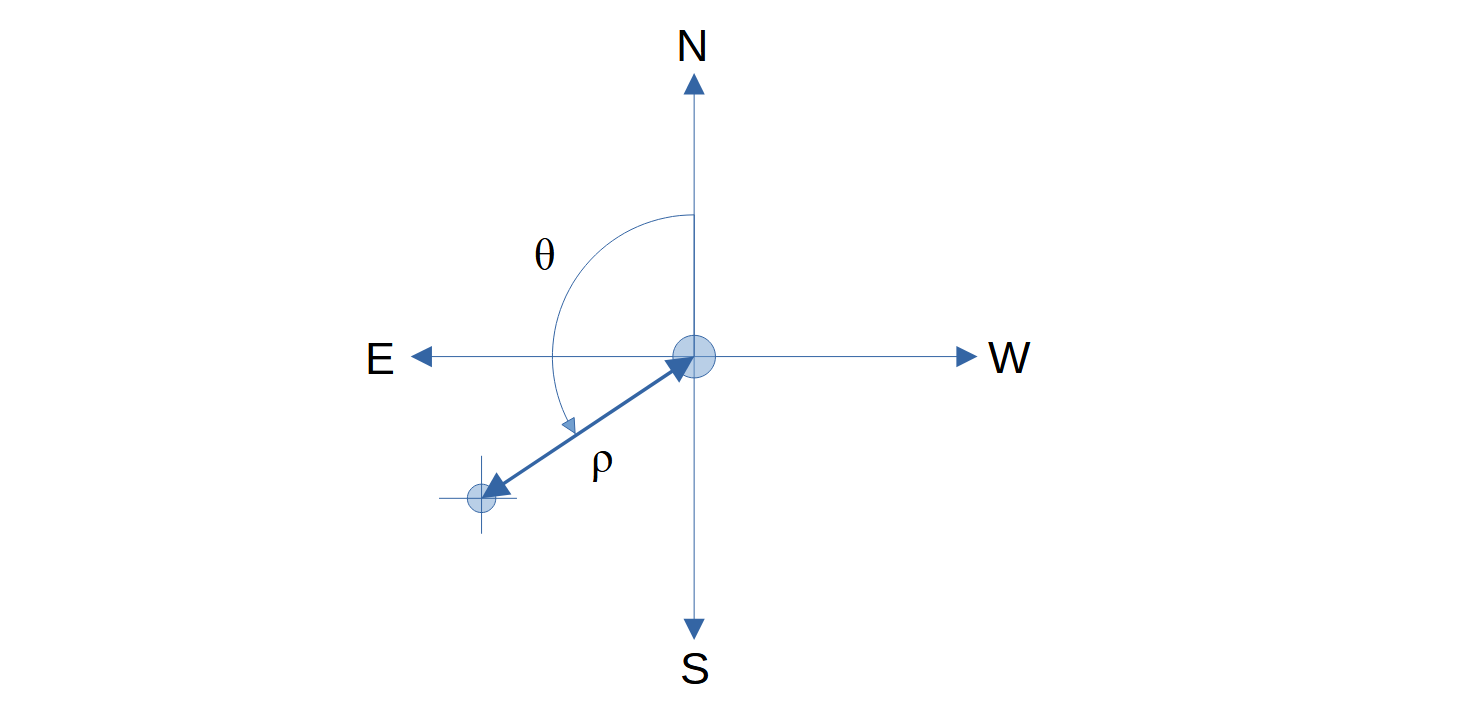
A distinction is made between optical and physical double or multiple stars. The former are stars that only happen to be in a line of sight, but are far behind each other in three-dimensional space and are not gravitationally bound. Physical binary and multiple stars are gravitationally bound.
Physical double stars can be divided into different categories. Visual double stars can be separated and measured with the naked eye or optical aids (binoculars, telescope). Spectroscopic double stars are so close together that they can no longer be separated with optical aids, but are noticeable in the spectrum through Doppler shifts. If the orbital plane of a double star system is aligned with the observer’s line of sight, one star may periodically pass in front of the other, causing mutual occultations similar to a solar eclipse. These occultations result in periodic variations in brightness, revealing the binary nature of the system. Such star pairs are known as eclipsing binaries. Finally, there are astrometric double stars, which only reveal themselves in the course of time due to a non-linear movement in the sky. Single stars have a constant motion in the sky, while astrometric double stars fluctuate periodically back and forth in their motion. Fluctuations in movement drew the attention of astronomers to Sirius B, for example.
To be distinguished from Double Stars are Common Proper Motion (CPM) Pairs. In addition to gravitationally bound double stars, there are pairs of stars known as Common Proper Motion (CPM) pairs. These are two or more stars that appear to move together through space, sharing the same proper motion. Unlike gravitationally bound systems, CPM pairs are not necessarily physically associated, and their apparent motion together is simply due to their being located along a similar line of sight or moving through space in the same direction. In contrast, gravitationally bound double stars follow more predictable orbital motions due to mutual gravitational attraction.
This chapter provides information and guidance on measuring the separation and position angle of double stars using amateur equipment and small telescopes with fairly high accuracy.
The content is available for download as a PDF document and is published under the Creative Commons license CC BY-NC-SA 4.0.
The document has been developed over several years and reflects my knowledge on the subject, primarily acquired during this time. Any errors or inaccuracies within the document are the responsibility of the author. Constructive feedback is always welcome and appreciated!
➔ Double Stars: Measurement of Distance and Position Angle with Small Telescopes
| Tool | Revision | Change |
| DS-CALC | 1873 | Changed formula of cCalculation of sepa |
| DS-CALC | 1867 | Two CPM Evidence calculation methods added, acc. to Harshaw and acc.to DSC |
| DS-CALC | 1829 | HRD added to DS-CALC |
| DS-CALC | 1747 | Orbit Determination improved, Online-Help updated, WDS notes decoding added |
| DS-ORBITD | 1734 | First off - Orbit Determination, Online-Help updated |
| DS-CALC | 1703 | Changed from WDS text file to SQL database |
| DS-CALC | 1692 | Added separation, CPM, and binding evidence factors; calculation of projected separation is now based on the nearer star; common style sheets introduced |
| DS-CALC | 1455 | Bugfixes, Bot/Scanner protection improved |
| DS-CALC | 1378 | Changed default double star to STF 1872 AB |
| DS-CALC | 1350 | Improved search function in WDS DB |